西関 隆夫 教授と水木 敬明 助教授が
平成17年度 国際コミュニケーション基金優秀研究賞を受賞
|
|
平成18年4月25日、
西関隆夫教授(システム情報科学専攻)と水木敬明助教授(応用情報科学専攻)が
平成17年度 国際コミュニケーション基金優秀研究賞を受賞しました。
■受賞研究題目: 絶対に安全な秘密鍵共有の通信プロトコル
■研究内容概説:
小学校の算数の問題
「整数35を素因数分解しなさい」 に対し、誰でも
35=5×7
と直ちに答えることができます。では7桁の大きな整数2,795,519ならば、いかがでしょうか。2,795,519は
2で割り切れないから、2は因子ではない。3でも割り切れないから、3も因子でない。4でも割り切れない
ので、4も因子でない。5でも割り切れないから、5も因子でない。このように小さい数字から順々に割り切
れるかどうか根気よく試していけば、683でやっと割り切れることがわかり、
2,795,519=683×4,093
と素因数分解が求まります。このように計算時間を気にしないならば、どんな大きい整数でも素因数分解
を求めることが原理的にはできます。しかし、300桁もの大きい整数になると、スーパーコンピュータで10年
間計算しても素因数分解を求めることが(計算量的に)困難になります。
今日、安全に通信するために暗号が用いられていますが、現在利用されている暗号のほとんどは、その
安全性の根拠を上に述べた素因数分解の計算量的な困難さ等に依存しており、解読アルゴリズムの発見
やコンピュータの高速化などにより、将来にわたり安全であるとは言えません。それに対して、本研究では、
絶対に安全な暗号に取り組んでおります。これは、情報理論的に安全な暗号とも呼ばれ、盗聴者がいかな
る計算能力・計算資源を持とうとも、安全な暗号のことです。そのような暗号の送受信者AliceとBobは、二
人だけが知っていて盗聴者には知られていない秘密の鍵を共有しないといけません。問題はいかにして
秘密鍵を絶対に安全に共有するかです。計算量的に安全に秘密鍵を共有する場合とは異なり、絶対的に
安全に秘密鍵を共有するためには、あらかじめAliceとBobに何らかの初期情報を与えておく必要がありま
す。そのような初期情報の一例として、トランプのようなカードをAliceとBobにランダムに配布しておくことが
考えられます。このため、カードのランダム配布によって秘密鍵を共有する問題が研究されてきましたが、
未解決な問題が数多く残されておりました。本研究では、これらの重要な問題に取り組み、それらのいくつ
かを解決しています。
AliceとBobが秘密鍵を共有したいとしましょう(図1)。しかし盗聴者Eveがいて、スーパーコンピュータを
1億台も持っており、無限の計算能力があるとします。そのため上述の初期情報(手品のタネ)が必要で
す。それがカードのランダム配布です。合計d 枚のカードには1からd までの異なる数字が書かれてあり、
よくカードをきってから、Aliceにa 枚、Bobにb 枚、Eveにe 枚配られてあったとします。つまり、盗聴者Eveは
既にe 枚のカードを盗聴できているとします。このような状況下で、AliceとBobはある種のトランプゲームを
行い、盗聴者Eveに知られないようにして、できるだけ長いビット数の秘密鍵を共有したいわけです。このト
ランプゲームのルールが「秘密鍵共有の通信プロトコル」です。
本研究では、AliceとBobにできるだけ長いビット数の秘密鍵を共有させるために、新しいプロトコル(ゲー
ムルール)を設計しました。詳細は省略しますが、AliceとBobは配られたカードを用いて、乱数を利用しなが
らトランプゲームを行い、盗聴者Eveのカードを含まないカードの山を作っていきます。図1にその流れを図示
しました。それらの山からAliceとBobは秘密鍵を共有することができるわけです。
AliceとBobが共有できる秘密鍵のビット数は、むろん配布されたカードの枚数a ,b ,e に依存しますが、
発生させる乱数の値にも依存します。本研究では、最も少ない場合のビット数k を、a ,b ,e から計算する
式を求めることができました。したがって、最悪の場合でも、AliceとBobはk ビット以上の秘密鍵を共有でき
ることになります。また、その式が最良であることも示すことができました。ちなみに、a
= b の場合には、
合計枚数d に対する盗聴者Eveの枚数e の割合e/d をパラメータにすると、d に対してkは図2のようになる
ことがわかりました。
この他にも本研究では、量子暗号を利用したメンタルポーカープロトコルを設計したり、結託攻撃に対する
電子透かしの安全性の新しい評価基準を導入し、その安全性の限界を示したりしております。それらの詳
細は省略します。
なお本研究で発表した5編の論文は博士後期課程院生 小泉康一氏(現在福島高専講師)、博士前期
課程院生 折原慎吾氏(現在NTT)および伴野幸造氏(現在東芝)との共著であり、一緒に楽しく研究できた
ことに感謝いたします。
|
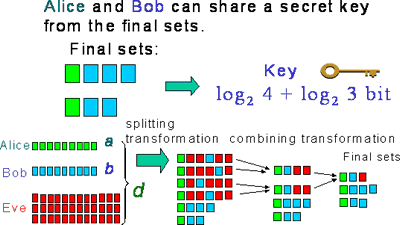 |
| 図1 新しいプロトコルによる鍵共有の流れ |
|
 |
| 図2 配布枚数d と共有ビット数k の関係 |
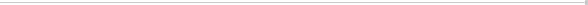 |
|