|
トップページ > 在学生の現状 > 学生の受賞 > 伊藤 健洋
第4回「研究科長賞」受賞
|
|
伊藤健洋さん
(システム情報科学専攻 博士課程後期3年の課程)
博士学位論文題目 :
Algorithms for Partitioning and Coloring Graphs
(グラフの分割と彩色に関する研究)
|
|
 |
| 伊藤 健洋 さん |
■受賞の感想
卒業に際し、研究科長賞という素晴らしい賞をいただき、たいへん光栄に思っています。
大学院での研究をこのような賞という形で飾ることができた喜びはひとしおです。これも西関教授、
周助教授をはじめとする諸先生方から懇切丁寧な御指導をいただいたおかげです。情報科学
研究科にはのびのびと研究に打ち込める環境があり、時には行き詰まって苦しいときもありましたが、
たいへん楽しい研究生活および学生生活を送ることができました。また、私を公私共に支えてくれた
研究室の先輩・後輩や、友人、家族にも感謝しています。この賞を励みとして、これからも研究に取
組んでいきたいと思います。
|
■研究内容
私はグラフアルゴリズムの研究を行ってきました。グラフとは、いくつかの点と、それらの点同士を
結ぶ何本かの辺からなるもので、いろいろな構造を抽象的に表現することに優れています。例えば、
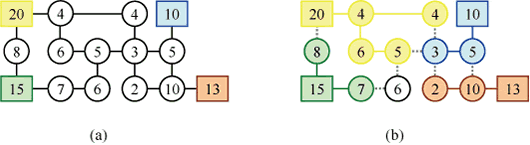
コンピュータネットワークや電力網の構造はグラフを用いて表現することができます。図(a)は電力網を
グラフで表現した例であり、各点は四角もしくは丸で描かれ、各辺は直線分で描かれています。
ここで、四角の点は発電所を表し、丸の点は負荷区間を表し、各辺は送電線を表しています。
現在、様々な問題がグラフを用いてモデル化されています。しかし、多くの問題は、複雑な構造をした
グラフに対しては効率よく解くことはできなく、現存するコンピュータで厳密に解こうとすると我々の寿命
よりも長い時間がかかってしまいます。そこで,構造がある程度制限されたグラフに対して、効率のよい
アルゴリズムを開発することが望まれています。私は特に“部分k -木”と呼ばれるグラフを扱いました。
部分k -木は、制限されたグラフとはいえ、実社会におけるコンピュータネットワークや電力網などはほと
んど全てが部分k -木であります。このようなグラフに対し、4つのテーマに基づく研究を行いましたが、
今回はそのうちの1つを説明します。
それは、電力系統の配電融通問題などに応用がある「需要点と供給点があるグラフの分割問題」です。
配電融通問題とは、ある負荷区間で停電が起きたとき、送電線のスイッチングを切り替えて周りの
発電所の余力を用いることにより、その停電を解消もしくは最小化したいという問題です。配電融通
問題の理論的な解法は確立されておらず、オペレータの経験則で解かれているのが現状です。そこで、
グラフの各点に需要点もしくは供給点の役割を持たせることにより電力網をグラフで表現し、配電融通
問題をグラフの分割問題としてモデル化しました。即ち、各需要点は負荷区間に対応し、各供給点は
発電所に対応し、各辺はスイッチングのできる送電線に対応します。また、各需要点には必要とする
電力量を表す「需要量」が割当てられ、各供給点には供給可能な電力量を表す「供給量」が割当てら
れます。そのようなグラフを用いて、できるだけ多くの負荷区間に電力を供給するスイッチングを見つける
問題を考えました。例えば,図(a)のグラフに対し、図(b)はスイッチングの一例を示しています。ここで、
各供給点は四角で描かれ、各需要点は丸で描かれ、各辺は直線分で描かれています。また、オフに
された送電線(辺)は点線で描かれています。このようなスイッチングを見つける問題は、非常に単純な
グラフに限定しても効率よく解けそうにない事が証明できます。そこで、問題を厳密に解くのではなく、
任意の精度の近似解を効率よく求める手法を開発しました。
この他にも、選挙区割問題に応用があるグラフの均一分割問題や、周波数割当問題に応用がある
距離辺彩色問題、並列タスクスケジューリングに応用がある多重彩色問題などを扱いましたが、
詳細は省略いたします。
|
 |
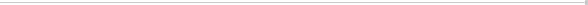 |
|